PID

PID control is a widely used control method in the 3D printing world. It’s ubiquitous when it comes to temperature control, be it with heaters to generate heat or fans to remove heat. This document aims to provide a high-level overview of what PID is and how to use it best in Klipper.

PID Calibration

Preparing the Calibration

When a calibration test is performed external influences should be minimized as much as possible:

• Turn off aux fans
• Turn off chamber heaters
• Turn off the extruder heater when calibrating the bed and vice versa
• Avoid external disturbances like drafts, etc.

More important than listed above, PID how you print. If your part fans are on when printing, PID tune with them on.

Choosing the right PID Algorithm

Klipper offers two different PID algorithms: Positional and Velocity

• Positional (pid) * The standard algorithm * Very robust against noisy temperature readings * Can cause overshoots * Insufficient target control in edge cases
• Velocity (pid_v) * No overshoot * Better target control in certain scenarios * More susceptible to noisy sensors * Might require larger smoothing time constants

Refer to the control statement in the Configuration Reference.

Running the PID Calibration

The PID calibration is invoked via the PID_CALIBRATE command. This command will heat up the respective heater and let it cool down around the target temperature in multiple cycles to determine the needed parameters.

Such a calibration cycles looks like the following snippet:

3:12 PM   PID_CALIBRATE HEATER=extruder TARGET=220 TOLERANCE=0.01 WRITE_FILE=1
3:15 PM   sample:1 pwm:1.0000 asymmetry:3.7519 tolerance:n/a
3:15 PM   sample:2 pwm:0.6229 asymmetry:0.3348 tolerance:n/a
3:16 PM   sample:3 pwm:0.5937 asymmetry:0.0840 tolerance:n/a
3:17 PM   sample:4 pwm:0.5866 asymmetry:0.0169 tolerance:0.4134
3:18 PM   sample:5 pwm:0.5852 asymmetry:0.0668 tolerance:0.0377
3:18 PM   sample:6 pwm:0.5794 asymmetry:0.0168 tolerance:0.0142
3:19 PM   sample:7 pwm:0.5780 asymmetry:-0.1169 tolerance:0.0086
3:19 PM   PID parameters: pid_Kp=16.538 pid_Ki=0.801 pid_Kd=85.375
               The SAVE_CONFIG command will update the printer config file
               with these parameters and restart the printer.

Note the asymmetry information. It provides an indication if the heater's power is sufficient to ensure a symmetrical "heat up" versus "cool down / heat loss" behavior. It should start positive and converge to zero. A negative starting value indicates that the heat loss is faster than the heat up, this means the system is asymmetrical. The calibration will still be successful but reserves to counter disturbances might be low.

Advanced / Manual Calibration

Many methods exist for calculating control parameters, such as Ziegler-Nichols, Cohen-Coon, Kappa-Tau, Lambda, and many more. By default, classical Ziegler-Nichols parameters are generated. If a user wants to experiment with other flavors of Ziegler-Nichols, or Cohen-Coon parameters, they can extract the constants from the log as seen below and enter them into this spreadsheet.

Ziegler-Nichols constants: Ku=0.103092 Tu=41.800000
Cohen-Coon constants: Km=-17.734845 Theta=6.600000 Tau=-10.182680

Classic Ziegler-Nichols parameters work in all scenarios. Cohen-Coon parameters work better with systems that have a large amount of dead time/delay. For example, if a printer has a bed with a large thermal mass that’s slow to heat up and stabilize, the Cohen-Coon parameters will generally do a better job at controlling it.

Further Readings

History

The first rudimentary PID controller was developed by Elmer Sperry in 1911 to automate the control of a ship's rudder. Engineer Nicolas Minorsky published the first mathematical analysis of a PID controller in 1922. In 1942, John Ziegler & Nathaniel Nichols published their seminal paper, "Optimum Settings for Automatic Controllers," which described a trial-and-error method for tuning a PID controller, now commonly referred to as the "Ziegler-Nichols method.

In 1984, Karl Astrom and Tore Hagglund published their paper "Automatic Tuning of Simple Regulators with Specifications on Phase and Amplitude Margins". In the paper they introduced an automatic tuning method commonly referred to as the "Astrom-Hagglund method" or the "relay method".

In 2019 Brandon Taysom & Carl Sorensen published their paper "Adaptive Relay Autotuning under Static and Non-static Disturbances with Application to Friction Stir Welding", which laid out a method to generate more accurate results from a relay test. This is the PID calibration method currently used by Klipper.

Details of the Relay Test

As previously mentioned, Klipper uses a relay test for calibration purposes. A standard relay test is conceptually simple. You turn the heater’s power on and off to get it to oscillate about the target temperature, as seen in the following graph.

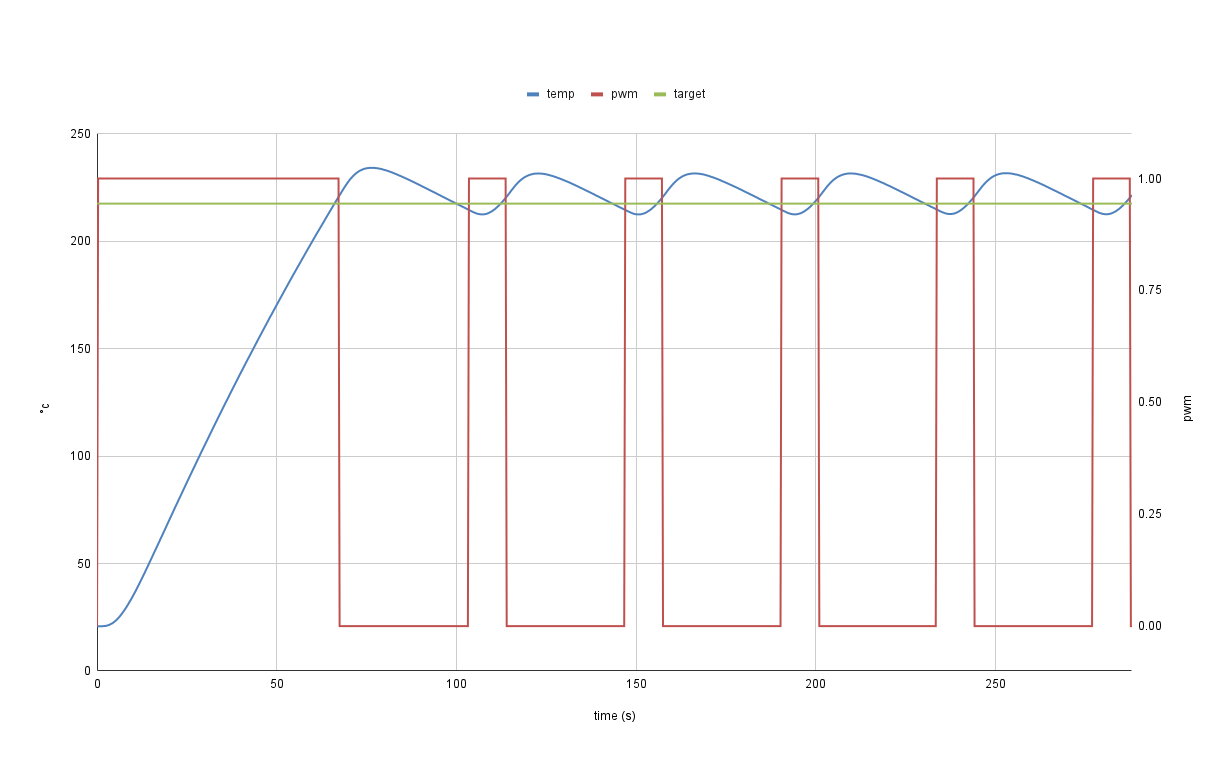
The above graph shows a common issue with a standard relay test. If the system being calibrated has too much or too little power for the chosen target temperature, it will produce biased and asymmetric results. As can be seen above, the system spends more time in the off state than on and has a larger amplitude above the target temperature than below.

In an ideal system, both the on and off times and the amplitude above and below the target temperature would be the same. 3D printers don’t actively cool the hot end or bed, so they can never reach the ideal state.

The following graph is a relay test based on the methodology laid out by Taysom & Sorensen. After each iteration, the data is analyzed and a new maximum power setting is calculated. As can be seen, the system starts the test asymmetric but ends very symmetric.

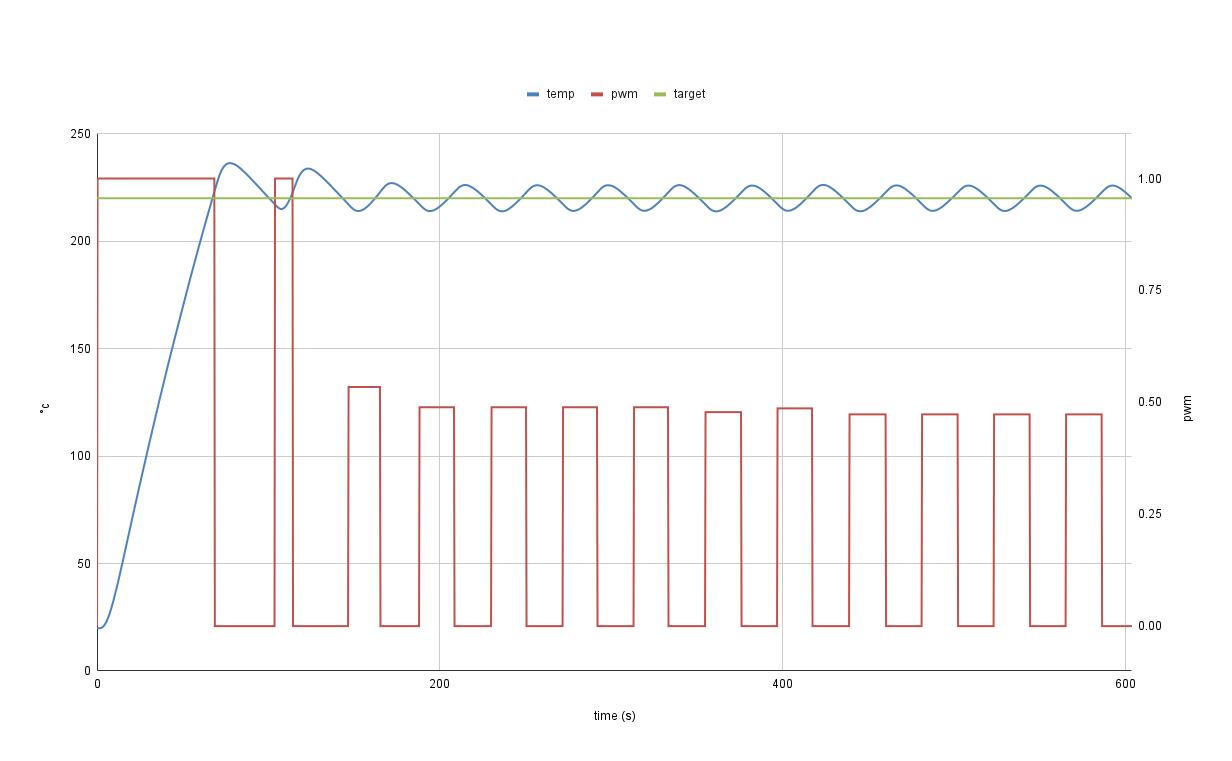
Asymmetry can be monitored in real time during a calibration run. It can also provide insight into how suitable the heater is for the current calibration parameters. When asymmetry starts off positive and converges to zero, the heater has more than enough power to achieve symmetry for the calibration parameters.

3:12 PM   PID_CALIBRATE HEATER=extruder TARGET=220 TOLERANCE=0.01 WRITE_FILE=1
3:15 PM   sample:1 pwm:1.0000 asymmetry:3.7519 tolerance:n/a
3:15 PM   sample:2 pwm:0.6229 asymmetry:0.3348 tolerance:n/a
3:16 PM   sample:3 pwm:0.5937 asymmetry:0.0840 tolerance:n/a
3:17 PM   sample:4 pwm:0.5866 asymmetry:0.0169 tolerance:0.4134
3:18 PM   sample:5 pwm:0.5852 asymmetry:0.0668 tolerance:0.0377
3:18 PM   sample:6 pwm:0.5794 asymmetry:0.0168 tolerance:0.0142
3:19 PM   sample:7 pwm:0.5780 asymmetry:-0.1169 tolerance:0.0086
3:19 PM   PID parameters: pid_Kp=16.538 pid_Ki=0.801 pid_Kd=85.375
               The SAVE_CONFIG command will update the printer config file
               with these parameters and restart the printer.

When asymmetry starts off negative, It will not converge to zero. If Klipper does not error out, the calibration run will complete and provide good PID parameters, However the heater is less likely to handle disturbances as well as a heater with power in reserve.

3:36 PM   PID_CALIBRATE HEATER=extruder TARGET=220 TOLERANCE=0.01 WRITE_FILE=1
3:38 PM   sample:1 pwm:1.0000 asymmetry:-2.1149 tolerance:n/a
3:39 PM   sample:2 pwm:1.0000 asymmetry:-2.0140 tolerance:n/a
3:39 PM   sample:3 pwm:1.0000 asymmetry:-1.8811 tolerance:n/a
3:40 PM   sample:4 pwm:1.0000 asymmetry:-1.8978 tolerance:0.0000
3:40 PM   PID parameters: pid_Kp=21.231 pid_Ki=1.227 pid_Kd=91.826
               The SAVE_CONFIG command will update the printer config file
               with these parameters and restart the printer.

Pid Control Algorithms

Klipper currently supports two control algorithms: Positional and Velocity. The fundamental difference between the two algorithms is that the Positional algorithm calculates what the PWM value should be for the current time interval, and the Velocity algorithm calculates how much the previous PWM setting should be changed to get the PWM value for the current time interval.

Positional is the default algorithm, as it will work in every scenario. The Velocity algorithm can provide superior results to the Positional algorithm but requires lower noise sensor readings, or a larger smoothing time setting.

The most noticeable difference between the two algorithms is that for the same configuration parameters, velocity control will eliminate or drastically reduce overshoot, as seen in the graphs below, as it isn’t susceptible to integral wind-up.

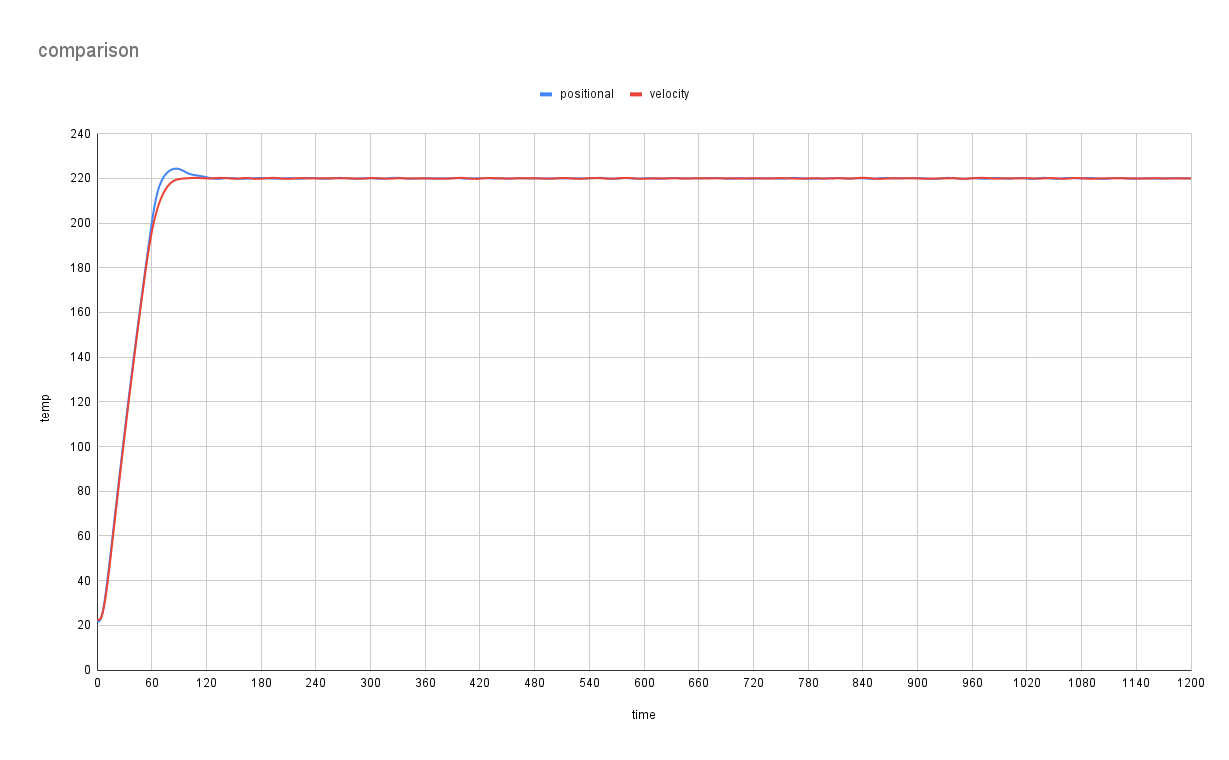
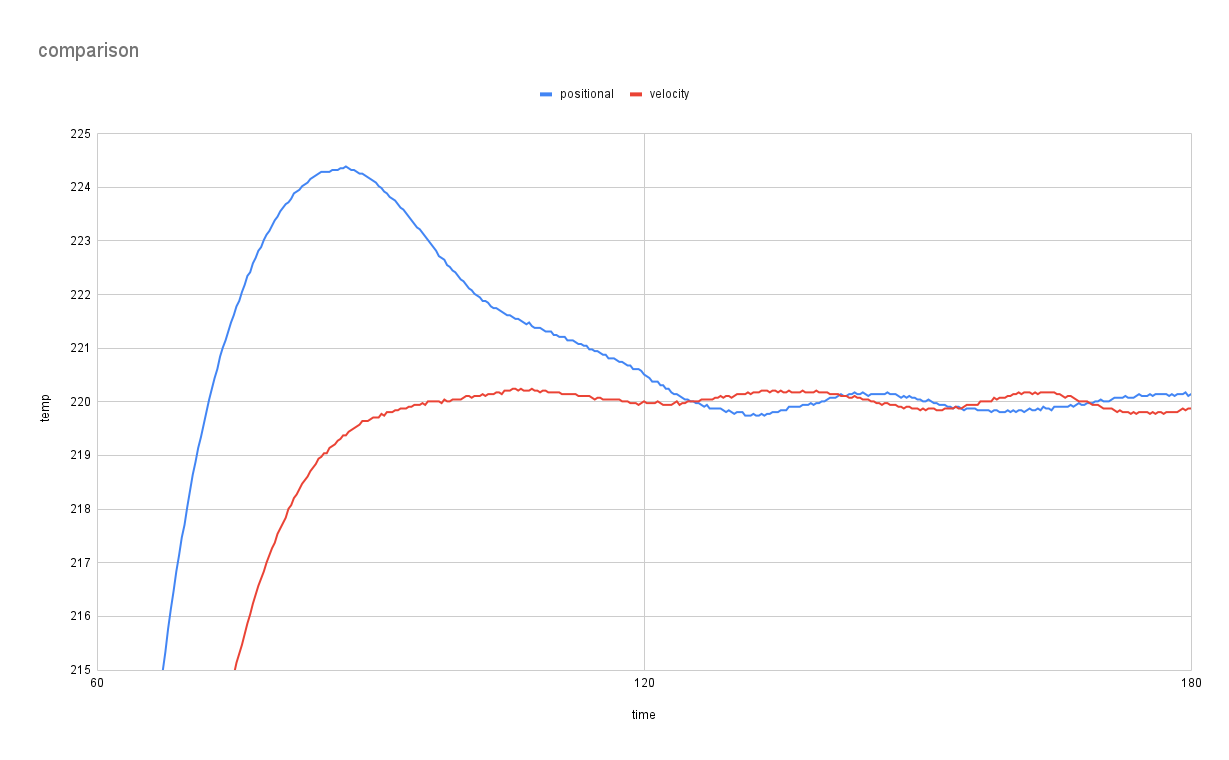
In some scenarios Velocity control will also be better at holding the heater at its target temperature, and rejecting disturbances. The primary reason for this is that velocity control is more like a standard second order differential equation. It takes into account position, velocity, and acceleration.